本篇内容
经典计数问题(分配问题) 整数的分割 Stirling number of the second 容斥原理 覆盖集# 1. 概念# 一个集合 A A A A 1 , A 2 , … , A n {A_1, A_2, \dots, A_n} A 1 , A 2 , … , A n ⋃ i = 1 n A i = A \bigcup_{i=1}^{n}A_i=A ⋃ i = 1 n A i = A A A A
2. 定理# 对于一个有限集合 A A A A 1 , A 2 , … , A n {A_1, A_2, \dots, A_n} A 1 , A 2 , … , A n A A A A i A_i A i A A A
归纳证明可以分为三个步骤:
当 n = 1 n=1 n = 1 假设当 n = k n=k n = k ( k ≥ 2 ) (k\geq2) ( k ≥ 2 ) ∣ A ∣ ≤ ∑ i = 1 k ∣ A i ∣ |A|\leq\sum_{i=1}^{k}|A_i| ∣ A ∣ ≤ ∑ i = 1 k ∣ A i ∣ 当 n = k + 1 n=k+1 n = k + 1 A k + 1 A_{k+1} A k + 1 A 1 , A 2 , … , A k {A_1, A_2, \dots, A_k} A 1 , A 2 , … , A k A 1 , A 2 , … , A k , A k + 1 {A_1, A_2, \dots, A_k, A_{k+1}} A 1 , A 2 , … , A k , A k + 1 A A A ⋃ i = 1 k + 1 A i = A \bigcup_{i=1}^{k+1}A_i=A ⋃ i = 1 k + 1 A i = A ∣ A ∣ ≤ ∑ i = 1 k ∣ A i ∣ + ∣ A k + 1 ∣ = ∑ i = 1 k + 1 ∣ A i ∣ |A|\leq\sum_{i=1}^{k}|A_i|+|A_{k+1}|=\sum_{i=1}^{k+1}|A_i| ∣ A ∣ ≤ ∑ i = 1 k ∣ A i ∣ + ∣ A k + 1 ∣ = ∑ i = 1 k + 1 ∣ A i ∣ 综上所述,对于一个有限集合 A A A A 1 , A 2 , … , A n {A_1, A_2, \dots, A_n} A 1 , A 2 , … , A n A A A
鸽子洞原理# 鸽子洞原理(Pigeonhole Principle)是离散数学中的一个基本原理,简言之,如果将 n + 1 n+1 n + 1 n n n 2 2 2
更一般地,如果有 N N N n n n ⌈ N n ⌉ \lceil \frac{N}{n} \rceil ⌈ n N ⌉
这个原理的证明可以这样理解:
如果有 n + 1 n+1 n + 1 n n n n n n n + 1 n+1 n + 1 2 2 2
同样地,如果有 N N N n n n ⌊ N n ⌋ \lfloor \frac{N}{n} \rfloor ⌊ n N ⌋ n ⋅ ⌊ N n ⌋ n \cdot \lfloor \frac{N}{n} \rfloor n ⋅ ⌊ n N ⌋ N − n ⋅ ⌊ N n ⌋ N - n \cdot \lfloor \frac{N}{n} \rfloor N − n ⋅ ⌊ n N ⌋ ⌈ N n ⌉ \lceil \frac{N}{n} \rceil ⌈ n N ⌉
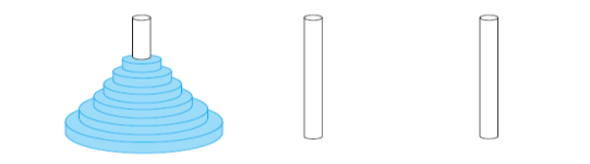
经典问题# 1. 汉诺塔问题# 汉诺塔问题是一个经典的数学谜题,也被称为汉诺威塔或汉诺塔。问题的设定是:有三个柱子,最左边的柱子上有 n n n
显然,对于 n = 1 n=1 n = 1 H 1 = 1 H_1=1 H 1 = 1 n = 2 n=2 n = 2 H 2 = 3 H_2=3 H 2 = 3 n ≥ 3 n\geq 3 n ≥ 3 n − 1 n-1 n − 1 n n n n − 1 n-1 n − 1 n − 1 n-1 n − 1 H n − 1 H_{n-1} H n − 1 n − 1 n-1 n − 1 H n − 1 H_{n-1} H n − 1 H n = 2 H n − 1 + 1 H_n=2H_{n-1}+1 H n = 2 H n − 1 + 1
2. 斐波那契数列# 斐波那契数列是一个数学序列,它的定义如下: f 0 = 1 , f 1 = 1 , f n = f n − 1 + f n − 2 ( n ≥ 2 ) f_0=1,\ f_1=1,\ f_n=f{n-1}+f_{n-2} (n\geq 2) f 0 = 1 , f 1 = 1 , f n = f n − 1 + f n − 2 ( n ≥ 2 )
对于斐波那契数列,可以通过递推公式 f n = f n − 1 + f n − 2 f_n=f_{n-1}+f_{n-2} f n = f n − 1 + f n − 2 f n f_n f n
3. 通项公式# 斐波那契数列的通项公式为 f n = 1 5 ( 1 + 5 2 ) n − 1 5 ( 1 − 5 2 ) n f_n=\frac{1}{\sqrt{5}}\left(\frac{1+\sqrt{5}}{2}\right)^n-\frac{1}{\sqrt{5}}\left(\frac{1-\sqrt{5}}{2}\right)^n f n = 5 1 ( 2 1 + 5 ) n − 5 1 ( 2 1 − 5 ) n
因此,如果要求解斐波那契数列中第 n n n
同样地,如果要求解汉诺塔问题中移动n n n H n H_n H n H n = 2 H n − 1 + 1 H_n=2H_{n-1}+1 H n = 2 H n − 1 + 1 H n = 2 n − 1 H_n=2^n-1 H n = 2 n − 1
线性齐次递推关系式# 线性齐次递推关系式(linear homogeneous recurrence relation)是一种数学函数序列。这个序列满足递推式:
a n = c 1 a n − 1 + c 2 a n − 2 + ⋯ + c k a n − k a_n=c_1a_{n-1}+c_2a_{n-2}+\cdots+c_k a_{n-k} a n = c 1 a n − 1 + c 2 a n − 2 + ⋯ + c k a n − k
其中 n ≥ k n\geq k n ≥ k c 1 , … , c k c_1,\dots,c_k c 1 , … , c k c k ≠ 0 c_k \neq 0 c k = 0
这种递推式的特点是:每个项都是前 k k k n n n
例如,f n = f n − 1 + f n − 2 f_n=f_{n-1}+f_{n-2} f n = f n − 1 + f n − 2 f n = 1 ⋅ f n − 1 + 1 ⋅ f n − 2 f_n=1\cdot f_{n-1}+1\cdot f_{n-2} f n = 1 ⋅ f n − 1 + 1 ⋅ f n − 2 H n = 2 H n − 1 + 1 H_n=2H_{n-1}+1 H n = 2 H n − 1 + 1
线性齐次递推关系式有许多应用,比如在计算机科学中,它们可以用来描述算法的时间复杂度。另外,对于一个线性齐次递推关系式,我们可以通过求解其特征方程来得到它的通项公式,进而计算出每一项的值。通常情况下,初始条件 a 0 , a 1 , … , a k − 1 a_0,a_1,\dots,a_{k-1} a 0 , a 1 , … , a k − 1
存在性和唯一性# 对于递推式 a n = ∑ i = 1 k c i a n − i a_n=\sum_{i=1}^{k}c_i a_{n-i} a n = ∑ i = 1 k c i a n − i x n {x_n} x n x i = a i x_i=a_i x i = a i 0 ≤ i < k 0\leq i<k 0 ≤ i < k
1. 存在性# 可以构造一个序列 x n {x_n} x n x n {x_n} x n k k k a n {a_n} a n x n {x_n} x n
2. 唯一性# 如果存在两个序列 x n {x_n} x n x n ′ {x_n'} x n ′ x n ≠ x n ′ x_n\neq x_n' x n = x n ′ n n n x n ≠ x n ′ x_n\neq x_n' x n = x n ′ k k k x n x_n x n x n ′ x_n' x n ′ n − k n-k n − k x n x_n x n x n ′ x_n' x n ′ n n n x n ≠ x n ′ x_n\neq x_n' x n = x n ′
综上所述,该定理保证了递推式的解的存在性和唯一性。这在离散数学中有着广泛的应用,例如在计算机科学中,递归和动态规划算法中常常需要求解递推式的解。
特征根# 特征根(characteristic roots),也称为特征值(eigenvalues),是解线性齐次递推关系式(Linear Homogeneous Recursive Relation,LHRR)的重要工具。对于 LHRR ,其递推关系式可以表示为 a n = ∑ i = 1 k c i a n − i a_n=\sum\limits_{i=1}^k c_i a_{n-i} a n = i = 1 ∑ k c i a n − i c i c_i c i a n a_n a n n n n
假设存在一种解形式为 a n = r n a_n=r^n a n = r n r n = ∑ i = 1 k c i r n − i r^n=\sum\limits_{i=1}^k c_i r^{n-i} r n = i = 1 ∑ k c i r n − i r n = c 1 r n − 1 + c 2 r n − 2 + ⋯ + c k r n − k r^n = c_1 r^{n-1} + c_2 r^{n-2} + \dots + c_k r^{n-k} r n = c 1 r n − 1 + c 2 r n − 2 + ⋯ + c k r n − k r r r
例如,在 LHRR , f n = f n − 1 + f n − 2 , n ≥ 2 f_n=f_{n-1}+f_{n-2}, n\geq 2 f n = f n − 1 + f n − 2 , n ≥ 2 r 2 − r − 1 = 0 r^2-r-1=0 r 2 − r − 1 = 0 r 1 = 1 + 5 2 r_1=\frac{1+\sqrt{5}}{2} r 1 = 2 1 + 5 r 2 = 1 − 5 2 r_2=\frac{1-\sqrt{5}}{2} r 2 = 2 1 − 5 f n = α 1 r 1 n + α 2 r 2 n f_n=\alpha_1 r_1^n+\alpha_2 r_2^n f n = α 1 r 1 n + α 2 r 2 n f n = f n − 1 + f n − 2 , n ≥ 2 f_n=f_{n-1}+f_{n-2}, n\geq 2 f n = f n − 1 + f n − 2 , n ≥ 2 α 1 \alpha_1 α 1 α 2 \alpha_2 α 2
特征根在线性代数和微分方程中也有广泛的应用。在矩阵的特征值分解中,特征根是矩阵特征值的通称。在微分方程的解法中,特征根是齐次线性微分方程的解形式。
线性非齐次递推关系式# 线性非齐次递推关系式(Linear Nonhomogeneous Recurrence Relation,LNRR)是指具有常系数和非零右端项的递推关系式,其中右端项可以是一个常数项或者是一个函数项。对于一个LNRR,可以找到对应的齐次递推关系式(Homogeneous Recurrence Relation,HRR),也称为其相关齐次递推关系式(Associated Homogeneous Recurrence Relation,AHRR)。AHRR 是一个不含右端项的齐次递推关系式。
一个 LNRR 的通项公式可以通过求解其对应的 AHRR 和特解(Particular Solution)相加得到。AHRR 的解可以表示为 a n = ∑ i = 1 k c i a n − i a_n=\sum\limits_{i=1}^k c_ia_{n-i} a n = i = 1 ∑ k c i a n − i c 1 , c 2 , … , c k c_1, c_2, \ldots, c_k c 1 , c 2 , … , c k c k ≠ 0 c_k\neq0 c k = 0 k k k
举个例子,对于 LNRR: a n = a n − 1 + a n − 2 + n 2 + n + 1 a_n=a_{n-1}+a_{n-2}+n^2+n+1 a n = a n − 1 + a n − 2 + n 2 + n + 1 a n = a n − 1 + a n − 2 a_n=a_{n-1}+a_{n-2} a n = a n − 1 + a n − 2 r 2 = r + 1 r^2=r+1 r 2 = r + 1 r 1 = 1 + 5 2 r_1=\frac{1+\sqrt{5}}{2} r 1 = 2 1 + 5 r 2 = 1 − 5 2 r_2=\frac{1-\sqrt{5}}{2} r 2 = 2 1 − 5 a n = c 1 r 1 n + c 2 r 2 n a_n = c_1 r_1^n + c_2 r_2^n a n = c 1 r 1 n + c 2 r 2 n c 1 c_1 c 1 c 2 c_2 c 2
接下来,我们需要求出特解。因为右端项是一个二次多项式,我们猜测特解是一个二次多项式 a n 2 + b n + c an^2+bn+c a n 2 + bn + c a a a b b b c c c
( a n 2 + b n + c ) − ( a ( n − 1 ) 2 + b ( n − 1 ) + c ) − ( a ( n − 2 ) 2 + b ( n − 2 ) + c ) = n 2 + n + 1 (an^2+bn+c)-(a(n-1)^2+b(n-1)+c)-(a(n-2)^2+b(n-2)+c)=n^2+n+1 ( a n 2 + bn + c ) − ( a ( n − 1 ) 2 + b ( n − 1 ) + c ) − ( a ( n − 2 ) 2 + b ( n − 2 ) + c ) = n 2 + n + 1
化简后,可以得到 a = 1 2 a=\frac{1}{2} a = 2 1 b = − 1 2 b=-\frac{1}{2} b = − 2 1 c = 1 c=1 c = 1 a n = 1 2 n 2 − 1 2 n + 1 a_n=\frac{1}{2}n^2-\frac{1}{2}n+1 a n = 2 1 n 2 − 2 1 n + 1
最终,我们得到了 LNRR 的通项公式 a n = c 1 r 1 n + c 2 r 2 n + 1 2 n 2 − 1 2 n + 1 a_n=c_1r_1^n+c_2r_2^n+\frac{1}{2}n^2-\frac{1}{2}n+1 a n = c 1 r 1 n + c 2 r 2 n + 2 1 n 2 − 2 1 n + 1 c 1 c_1 c 1 c 2 c_2 c 2
定理指出,如果 x n x_n x n y n y_n y n z n = x n + y n z_n=x_n+y_n z n = x n + y n
在这个定理中, y n y_n y n x n x_n x n y n = z n − x n y_n=z_n-x_n y n = z n − x n z n z_n z n x n x_n x n y n y_n y n z n = x n + y n z_n=x_n+y_n z n = x n + y n
总的来说,通解就是一类函数的一般形式,它包含了所有可能的特解。通解不是唯一的,因为可以通过加上任意一个与 LHRR 相关的解,得到另一个解。在实际应用中,我们需要选择一个特定的通解,以满足问题的初始条件或其他要求。