CS110 Project 4

Project 4

Computer Architecture I @ ShanghaiTech University

1. Introduction

First, read the code snippet below, which is a simple program that simulates heat conduction in a 2D plate.

for (k = 0; k < step; k++) {
    for (i = 1; i < N - 1; i++) {
        for (j = 1; j < N - 1; j++) {
            p_next[i * N + j] = (p[(i - 1) * N + j] + p[(i + 1) * N + j] + p[i * N + j + 1] + p[i * N + j - 1]) / 4.0;
        }
    }
    double *temp = p;
    p = p_next;
    p_next = temp;
}

Here, p and p_next are 2D arrays representing the current and next state of the plate, respectively. The loop iterates over each cell in the 2D array and calculates the next state based on the surrounding cells.

2. Getting started

Make sure you read through the entire specification before starting the project.

Just like all other programming assignments/projects this semester, you will obtain your files from the GitHub classroom, the link is here.

Files

The framework contains the following files:

test.c: Contains the test framework code.
baseline.c: Contains the baseline implementation.
impl.c: You need to complete the function impl(int N, int step, double *p). When the function returns, the array pointed to by p should contain the state after step iterations from its initial values. However, to enable more kinds of optimization techniques, there is a special formula to calculate the error between your implementation and the baseline implementation. Please READ THE FOLLOWING SECTION CAREFULLY, or you may LOSE POINTS!

Validation

We will calculate the error between the state of your p matrix and the baseline according to the following rules:

Assume the matrix side length is N and the number of iterations is step.
Let the result matrix after step iterations using the baseline algorithm be p^{step}, and the result after step-1 iterations be p^{step-1}. Denote the value at a point in the matrix as p_{i,j}.
For each point p_{i,j} in your p, the error is calculated as follows: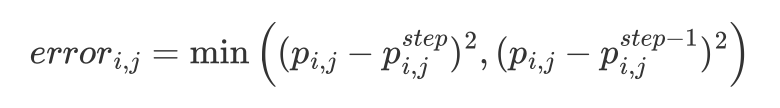
The total error is the sum of the errors of all points. Your total error should less than a certain value (1e-5 in the framework code). If you believe this precision requirement is too harsh, please contact us, and we may loosen the requirement based on our evaluation.

Example

Assuming the baseline's values after step iterations are as shown in the figure below:

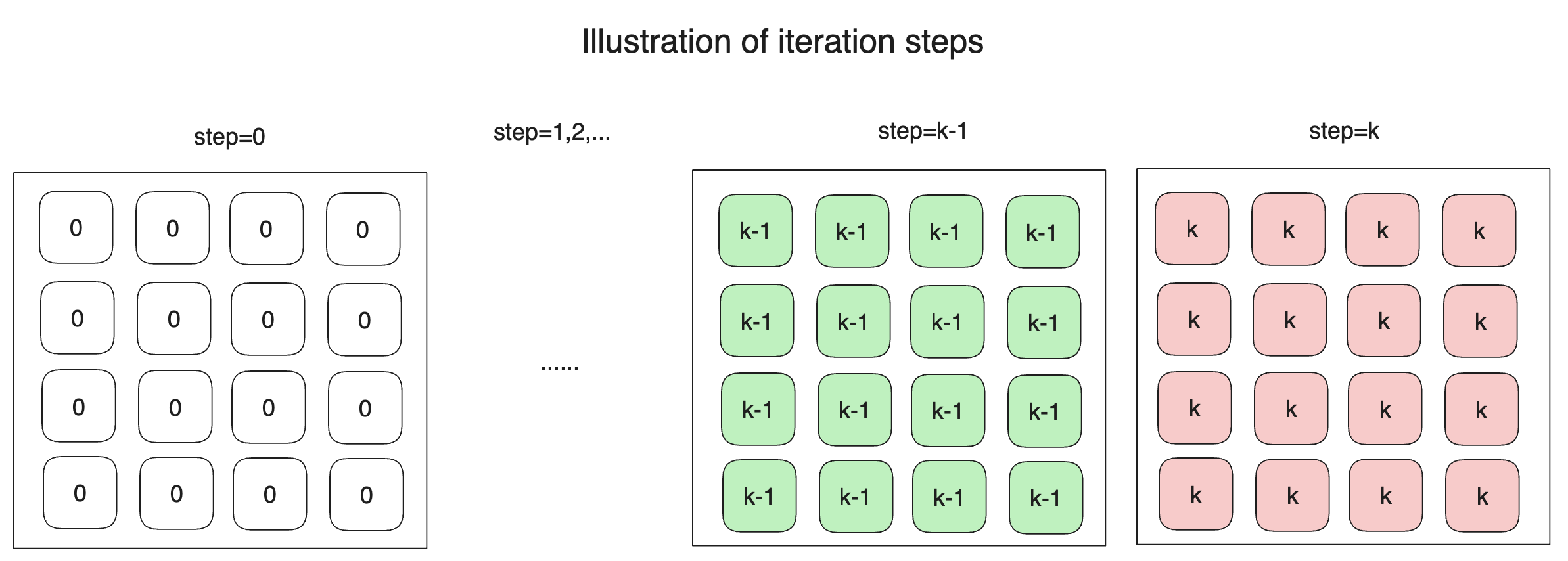
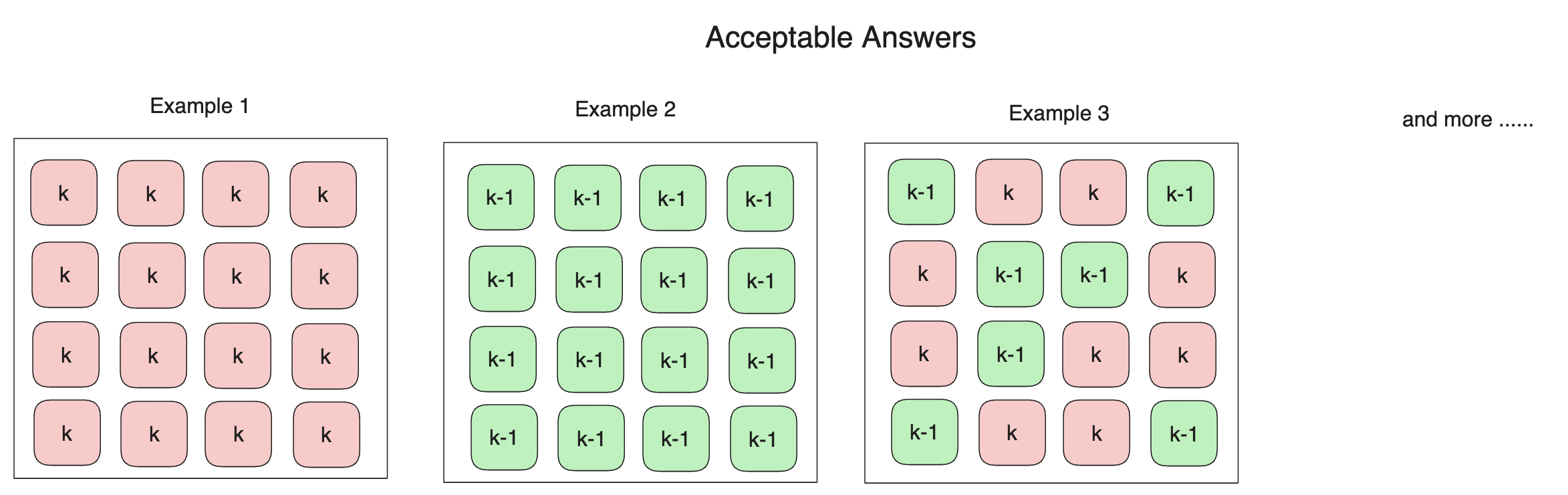
Then, as long as your result is close enough to any of the ones shown in the figure below (only partial examples are displayed), your result will be considered valid.

3. Optimization Techniques

You can find many obvious optimizations in the implementation we provide, based on what you have learned in Computer Architecture. We are listing some of the possible approaches below:

Compiler

There are some optimization flags that can be turned on in GCC. The available flags for x86 ISA from GCC are listed here. However, we hope that you can do most of the optimization yourself, instead of relying on the compiler. So in this project, you are not allowed to modify the Makefile.

Multithreading

The outer loop of the algorithm is a good candidate for multithreading. You can use OpenMP or pthread to parallelize.

SIMD instructions

SIMD processes multiple data in parallel. Part of this algorithm is also a good candidate for SIMD instructions.

Loop unrolling

Loop unrolling can be used to reduce the overhead of the loop.

Cache Blocking

The main idea here is to make memory access more efficient and exploit memory locality.

4. Grading Policy

The total score for this project is 100:

We will first run your code on small test cases on GradeScope (automatically). If your program does not produce the correct result, you will receive 0 points. As always, your code should not have any memory issues.
After the deadline, we will test your code on our local machine and new test cases. Your grade on this part depends on the speedup of your code. If your code runs slower than adding the baseline (what we've provided), you will receive 0 points.
If your code runs at the same speed with bare OpenMP, you will receive 50 points.
If your code ranks among the top 30 in performance in the class, you will receive 100 points.
For the rest, we will give a linear grade according to the speedup rate.
- If your speedup is 3.0 and the bare OpenMP speedup is 5.0, then your score will be (3.0 / 5.0) * 50 = 30.0 points.
- If your speedup is 7.3 and the bare OpenMP speedup is 5.0, while the 30th fastest code is 10.0 then your score will be 50 + ((7.3 - 5.0) / (10.0 - 5.0)) * 50 = 73.0 points.
If your code crashes during our test, you will receive 0 points.
Your submission must contain meaningful use of multithreading technique and Intel SIMD intrinsics. Otherwise, you will get 0 points. This check will be done manually after the deadline so there will be no feedback on this from GradeScope.

5. Parameters for Speed Test

For the final speed test, we will use a map with N=2000.

6. Server Configurations

The GrapeScope server is used for correctness check only because it has limited hardware resources and unstable performance.

Toast Lab Server (Used for final speed test):

CPU: Intel Xeon E5-2690 v4 2.6 GHz, 14 cores (28 threads) Details here
- L1 i-cache 32 KiB (per core)
- L1 d-cache 32 KiB (per core)
- L2 cache 3.5 MiB (unified)
- L3 cache 35 MiB (unified)
Memory: 120 GiB

More about the final speed test

The final test server in fact has two cpus that uses the NUMA architecture which is commonly used in modern servers. In the final test we will use numactl to run the program in a NUMA node. This is to avoid the impact of NUMA's memory arrangement on openmp. If you're interested, you can find out what numa is and why it has an effect on openmp. But we're not asking too much here, you can simply think of it as having only one CPU with 14 cores, as the same as the server configurations listed above.

Letong Han <hanlt AT shanghaitech.edu.cn>
Suting Chen <chenst AT shanghaitech.edu.cn>

Last modified: 2024-05-31